相关分析

相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析方法。通过对不同特征或数据间的关系进行分析，发现其中关键影响及驱动因素。在实际的工作应用中，常常用于特征的发现与选择。针对不同数据类型的变量，需要选用不同的检验方法，具体如下表所示

变量个数	变量类型	检验方法
两个	均为连续变量	皮尔逊相关系数、简单线性回归
两个	均为有序分类变量	Mantel-Haenszel 趋势检验、 Spearman相关、Kendall’s tau-b相关系数
两个	均为无序分类变量	卡方检验、Fisher精确检验
两个	均为二分类变量	相对风险、比值比、卡方检验和Phi (φ)系数、Fisher精确检验

皮尔逊相关系数

皮尔逊相关系数( Pearson correlation coefficient），又称皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，简称 PPMCC或PCCs），是用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间。

1.适用范围

• 两个变量之间是线性关系，都是连续数据。
• 两个变量的总体是正态分布，或接近正态的单峰分布。
• 两个变量的观测值是成对的，每对观测值之间相互独立。

2.原理

利用两个变量间的协方差和变量的标准差进行计算而来（分子是协方差，分母是两个变量标准差的乘积）

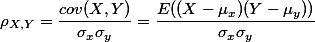
3.Python实现

import pandas as pd
import numpy as np

# 数据
# 这里求a\b\c\d与e的相关系数
df = pd.DataFrame(np.random.randn(20).reshape(4,5),index = [1,2,3,4],
                  columns=['a','b','c','d','e',])
x = df.values
correlation_matrix = np.corrcoef(x.T)
r = correlation_matrix[:, -1].tolist()
for i in range(len(r)):
	print(str(r[i]))

4.其他补充

为什么输出会有nan?

由于皮尔逊相关系数是利用两个变量间的协方差和变量的标准差进行计算而来，若相关系数为nan，说明数据存在问题

• 检查数据类型是否非数值型，可用info()
• 检查数据是否都一样，导致分母中的标准差为0

计算相关系数之前需不需要标准化?

不需要标准化，因为相关系数本来就是一个标准化的统计量，从上面的计算公式可见，这就是一个标准化的过程，即相关系数就是标准化了的协方差。